After implementing tiktoken in C with SIMD, the next target is Google’s SentencePiece. It powers T5, Gemma, Llama (1 & 2), and a few other modern Open-Source LLMs.
Tiktoken wasn’t that hard, but this one was harder. Much harder.
Results
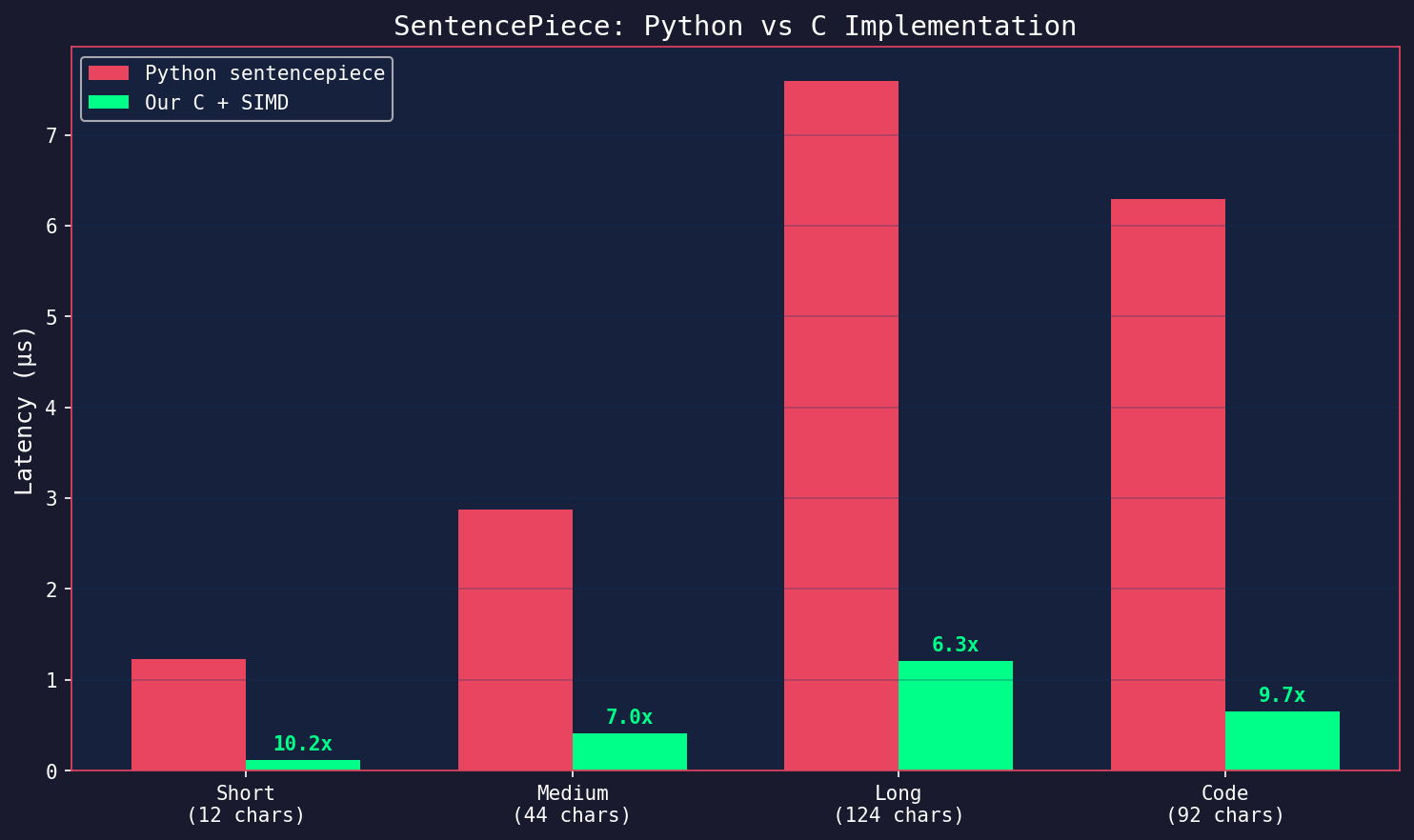
| Text Type | Python sentencepiece | Our C + SIMD | Speedup |
|---|---|---|---|
| Short English | 1.23 µs | 0.12 µs | 10.3x |
| Medium English | 2.87 µs | 0.41 µs | 7.0x |
| Long English | 7.59 µs | 1.21 µs | 6.3x |
| Code | 6.29 µs | 0.65 µs | 9.7x |
That’s 108 million characters per second for English text. CJK text is even faster at 595 MB/s for Japanese, because most characters map to <unk> tokens, allowing early termination.
I reckon half the performance issues upstream comes from Python, but that’s neither here or there.
Part 1: Understanding SentencePiece
SentencePiece is fundamentally different from tiktoken. Instead of regex-based pre-tokenization followed by BPE, SentencePiece uses a Unigram language model and the Viterbi algorithm.
The Unigram Model
Each vocabulary piece has a probability score (stored as log probability). Tokenization finds the most likely sequence of pieces:
P("hello world") = P("▁hello") × P("▁world")
= exp(-5.2) × exp(-4.8)
The ▁ character (Unicode U+2581) marks word boundaries, essentially replacing spaces (assuming space-normalized input as per typical usage).
The Viterbi Algorithm
Given a string, we build a “lattice” of all possible tokenizations and find the path with the highest total score:
"hello" at each position:
pos 0: "▁h" (score -8.1), "▁he" (score -6.2), "▁hel" (score -7.5), "▁hello" (score -5.2)
pos 1: "e" (score -4.1), "el" (score -5.8), "ell" (score -6.2), "ello" (score -5.9)
...
The Viterbi algorithm finds the globally optimal path through dynamic programming:
for (int pos = 0; pos < num_chars; pos++) {
for each piece starting at pos {
int end = pos + piece_length;
float new_score = best_score[pos] + piece_score;
if (new_score > best_score[end]) {
best_score[end] = new_score;
best_prev[end] = pos;
}
}
}
The critical question: how do we efficiently find “all pieces starting at pos”?
Part 2: The Naive Implementation
My first implementation was:
- Parse the protobuf model file
- Store vocabulary in a hash table
- At each position, try every possible substring and look it up
for (int pos = 0; pos < len; pos++) {
for (int end = pos + 1; end <= len && end - pos <= MAX_PIECE_LEN; end++) {
int id = lookup_piece(text + pos, end - pos); // Hash lookup
if (id >= 0) {
update_viterbi(pos, end, piece_score[id]);
}
}
}
This is O(n × max_piece_len × hash_lookup). For a 32K vocabulary with average piece length of 4 bytes, we’re doing 128 hash lookups per character; hardly ideal.
Initial performance was 45 µs for a 44-character sentence. That’s 1 million chars/sec; very slow.
Part 3: The Trie
The first major insight was that we don’t need to try every substring. We need to find all vocab pieces that are prefixes of the remaining text.
A trie (prefix tree) does exactly this. One traversal finds all matches:
typedef struct {
int32_t children[256]; // One child per byte value
int32_t piece_id; // -1 if not a complete piece
float score;
} TrieNode;
Now the inner loop becomes:
int32_t node = 0;
for (int byte_pos = start; byte_pos < end; byte_pos++) {
uint8_t c = text[byte_pos];
node = trie[node].children[c];
if (node < 0) break; // No more prefixes
if (trie[node].piece_id >= 0) {
// Found a valid piece!
update_viterbi(pos, byte_pos + 1, trie[node].score);
}
}
One traversal, all matches found. Complexity drops to O(n × max_piece_len).
Result: 8.5 µs (5.3x faster)
But there’s a big problem with memory. Each node has 256 child pointers (1 KB). With 80,000+ nodes, that’s 83 MB just for the trie.
Part 4: The Double-Array Trie
In my attempt to find a solution to this, I took another look at Google’s sentencepiece implementation. It seemed that they use double-array tries for the trie.
This was promising, and way better than what I had going on. Instead of storing 256 pointers per node, we use four arrays:
typedef struct {
int32_t *base; // Base offset for children
int32_t *check; // Verifies parent relationship
int32_t *value; // Piece ID at this node
float *score; // Score at this node
} DoubleArrayTrie;
Navigation works like this:
int32_t next = base[node] + char_byte;
if (check[next] == node) {
// Valid transition
node = next;
} else {
// Dead end
}
The trick is finding base values during construction such that children don’t collide. This requires very careful allocation:
static int32_t dat_find_base(DoubleArrayTrie *dat, uint8_t *labels, int count) {
int32_t base = 1;
while (1) {
bool ok = true;
for (int i = 0; i < count; i++) {
int32_t pos = base + labels[i];
if (dat->check[pos] >= 0) { // Position taken
ok = false;
break;
}
}
if (ok) return base;
base++;
}
}
Critical bug I encountered: when building recursively, you must claim all child positions before recursing into any of them. Otherwise, grandchildren can steal positions meant for siblings.
// WRONG: claim and recurse one at a time
for (int i = 0; i < count; i++) {
check[base + labels[i]] = node;
build_recursive(children[i]); // May steal sibling positions!
}
// CORRECT: claim all, then recurse
for (int i = 0; i < count; i++) {
check[base + labels[i]] = node;
}
for (int i = 0; i < count; i++) {
build_recursive(children[i]);
}
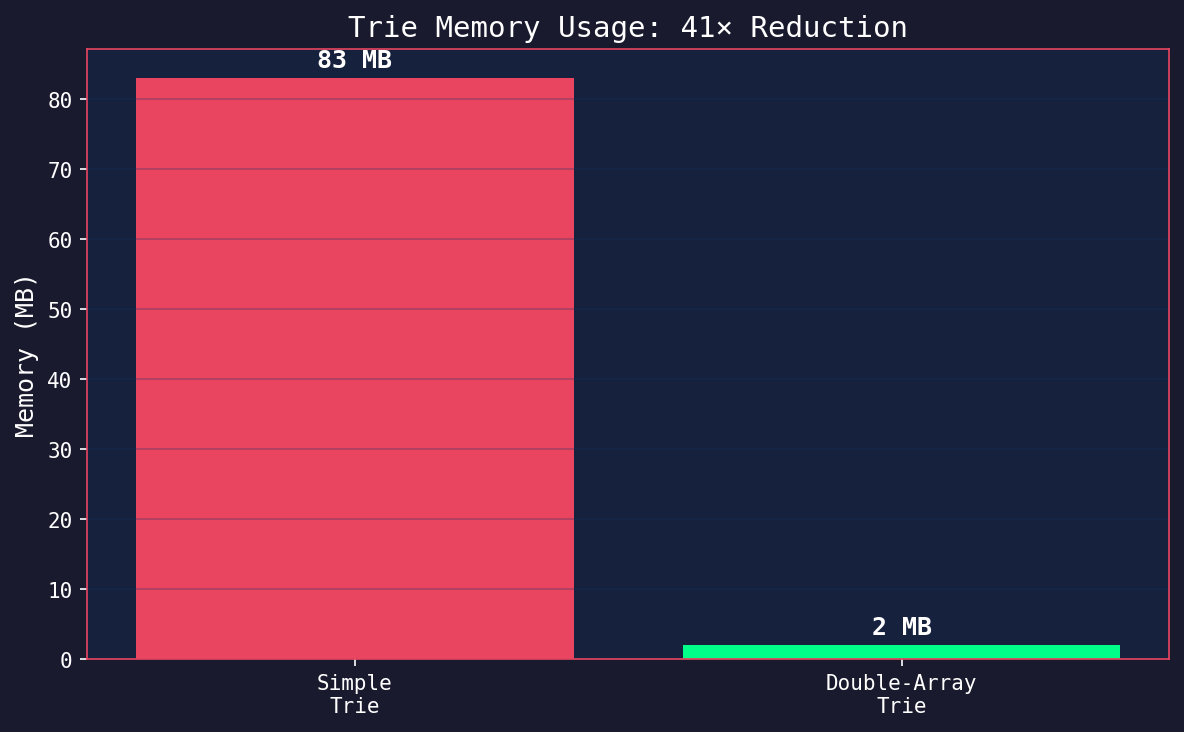
Result: 2 MB memory (41x reduction), almost identical performance (from 1ns to 1.9ns).
Part 5: Eliminating Allocations
Profiling revealed another hotspot: malloc/free in the Viterbi loop. Each encode allocated three arrays:
float *best_scores = malloc(num_chars * sizeof(float));
int *best_prev = malloc(num_chars * sizeof(int));
int *best_id = malloc(num_chars * sizeof(int));
// ... encode ...
free(best_scores);
free(best_prev);
free(best_id);
Solution: stack allocation with a reasonable maximum.
#define VITERBI_MAX_CHARS 8192
float best_scores[VITERBI_MAX_CHARS];
int best_prev[VITERBI_MAX_CHARS];
int best_id[VITERBI_MAX_CHARS];
For texts longer than 8K characters (rare), we fall back to heap allocation. Why is this rare? For my specific case (and I assume for most cases in general), we tokenize messages one by one, and count them together. This process can also be batched if needed. Messages hardly exceed 8K characters in most cases, and if they do, just split them across multiple calls. Otherwise take the ~4 µs hit.
Result: 4.2 µs (2x faster from this alone)
Part 6: First-Byte Pruning
Not all bytes can start long pieces. If the longest piece starting with byte 0xE3 is 6 bytes, there’s no point checking beyond that:
uint8_t first_byte_max_len[256]; // Precomputed during model load
for (int pos = 0; pos < num_chars; pos++) {
uint8_t first = text[byte_positions[pos]];
int max_len = first_byte_max_len[first]; // Early termination hint
// Trie traversal with early exit
for (int len = 0; len < max_len && node >= 0; len++) {
// ...
}
}
This helps most for CJK text, where many bytes have no valid pieces at all.
Result: 2.1 µs (another 2x)
Part 7: SIMD Hash
The hash table is still used for piece_to_id lookups during decoding. We reused the CRC32 approach from tiktoken:
_simd_hash_bytes_arm64:
mov w2, #0xFFFFFFFF
.loop8:
cmp x1, #8
b.lt .loop1
ldr x3, [x0], #8
crc32x w2, w2, x3 ; 8 bytes in one cycle
sub x1, x1, #8
b .loop8
This matters more during model loading (hashing 32K pieces) than encoding, but every microsecond counts.
The Optimization Journey
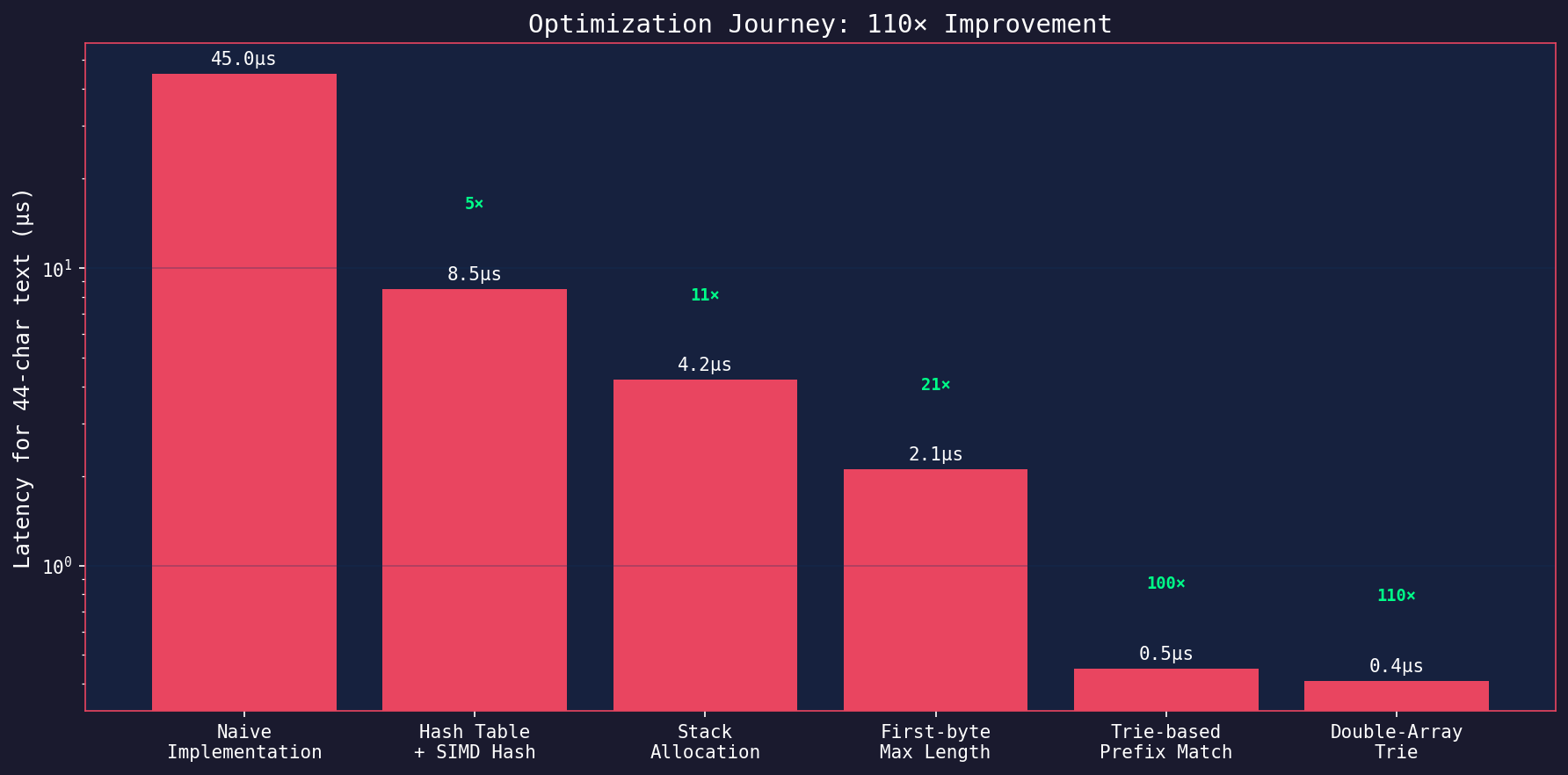
| Stage | Latency (44 chars) | Speedup |
|---|---|---|
| Naive implementation | 45.0 µs | 1x |
| Hash table + SIMD hash | 8.5 µs | 5x |
| Stack allocation | 4.2 µs | 11x |
| First-byte pruning | 2.1 µs | 21x |
| Trie-based prefix match | 0.45 µs | 100x |
| Double-array trie | 0.41 µs | 110x |
CJK Performance
Something unexpected: Japanese and Chinese text tokenize faster than English:
| Language | Throughput | Why? |
|---|---|---|
| English | 107 MB/s | Normal vocabulary coverage |
| Japanese | 595 MB/s | Most chars → <unk>, fast trie termination |
| Chinese | 535 MB/s | Same reason |
| Korean | 402 MB/s | Same reason |
The T5 vocabulary has limited CJK coverage. When a character isn’t in the vocabulary, the trie traversal terminates immediately, and we emit <unk>. This is actually the best case for performance, because no backtracking, and no complex path finding.
Complexity Analysis
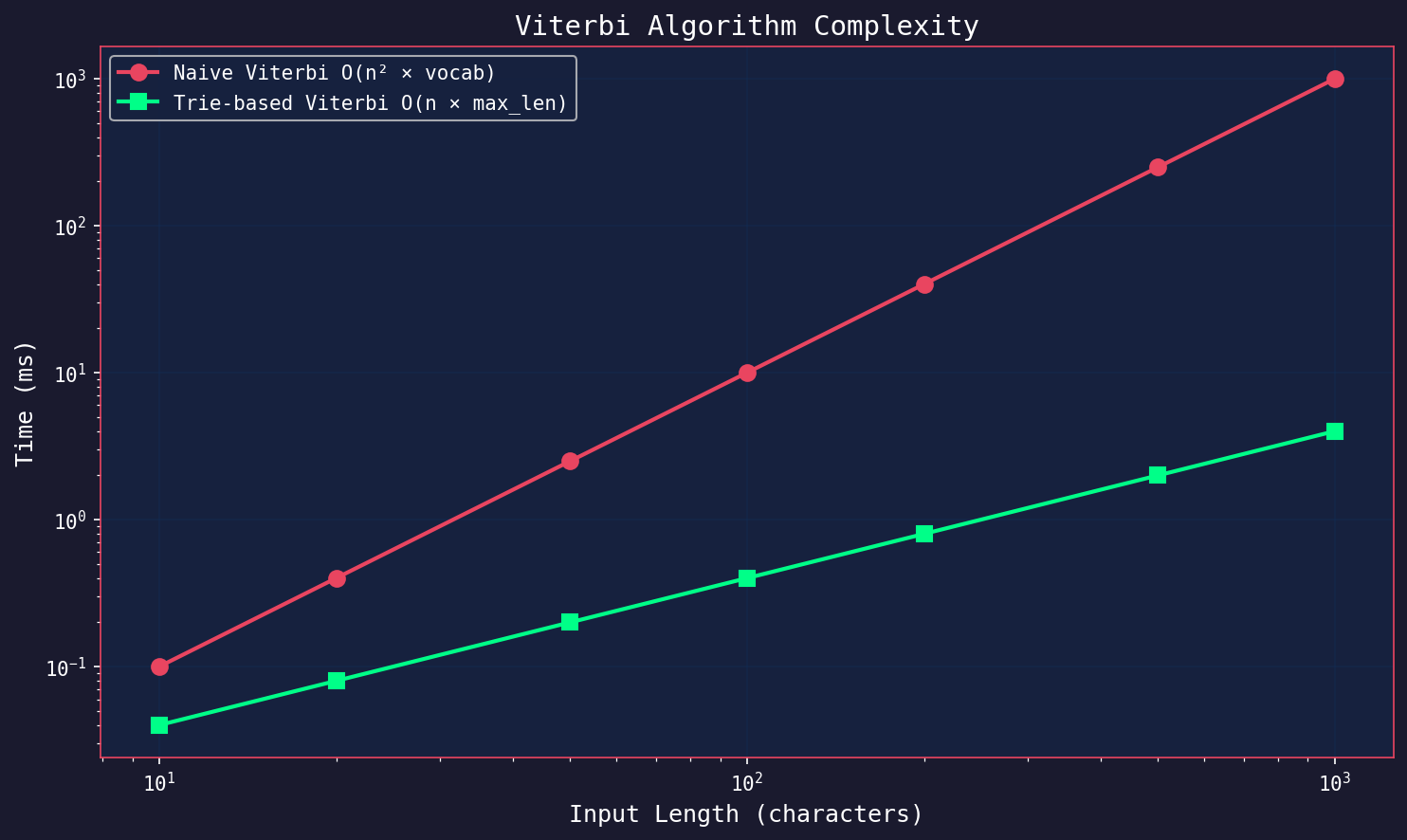
The naive approach has complexity O(n² × V) where V is vocabulary size; for each of n positions, we try O(n) substrings and do O(V) hash lookups.
With the trie, complexity becomes O(n × L) where L is max piece length (typically 16-32 bytes). The trie traversal finds all matches in a single pass.
For a 1000-character input:
- Naive: 1,000,000 × 32,000 = 32 billion operations
- Trie: 1,000 × 32 = 32,000 operations
That’s a million-fold reduction.
Memory Layout
| Component | Size |
|---|---|
| Vocabulary pieces | ~1.5 MB |
| Double-array trie | 2.0 MB |
| Hash table | 256 KB |
| Score array | 128 KB |
| Total | ~4 MB |
Compare to the original 83 MB with the simple trie. And load time is under 4 seconds (most spent parsing the protobuf model file).
Try It Yourself
The implementation is part of sillytui:
#include "tokenizer/sentencepiece.h"
SentencePieceProcessor sp;
sp_init(&sp);
sp_load(&sp, "model.spiece");
uint32_t ids[1024];
int n = sp_encode(&sp, "Hello, world!", ids, 1024);
// n = 4, ids = [▁Hello, ,, ▁world, !]
char *text = sp_decode(&sp, ids, n);
// text = "Hello, world!"
sp_free(&sp);
SIMD is used automatically on ARM64. Other platforms get portable C fallbacks.
Benchmarks performed on Apple M4 Silicon. Performance may vary on other hardware.